| Переглянути всі підручники | |||||||||||||
| << | < | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | > | >> |
на множині всіх дійсних чисел. Описаним у попередньому параграфі способом побудуємо графіки даних функцій (мал. 45 і 46). Бачимо, що графік кожної з розглядуваних функцій — пряма. Можна довести, що графік кожної лінійної функції — пряма. І кожна пряма на координатній площині, не перпендикулярна до осі абсцис,— графік деякої лінійної функції.
Графік лінійної функції є водночас графіком деякого лінійного рівняння з двома змінними (лінійні рівняння і їх графіки розглядались у 7 класі). Наприклад, рівняння Зх + 2і/ = 6 і г/=—1,5х + 3 рівносильні, їм відповідають однакові графіки. Тому пряма, яка є графіком рівняння Зх-\-2у = 6, є також графіком функції, заданої формулою y——l,5x-\-S.
Оскільки графік кожної лінійної функції — пряма, для його побудови досить знати координати двох його точок. Наприклад, щоб побудувати графік функції

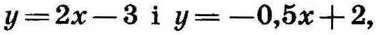
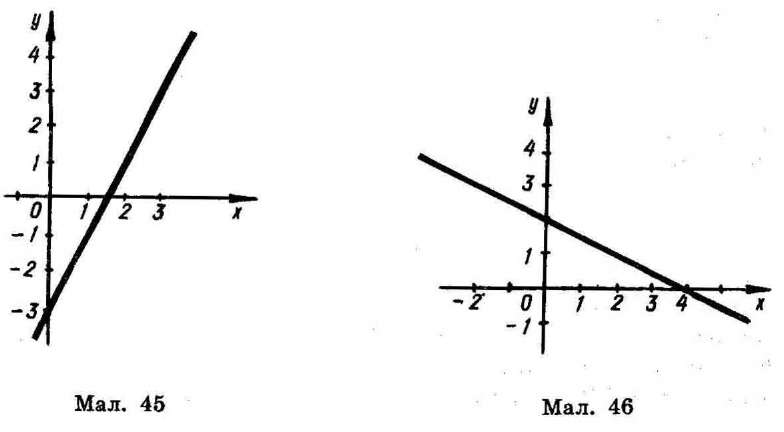
| Переглянути всі підручники | |||||||||||||
| << | < | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | > | >> |